I don’t know how to install graphite and graphite web to make graphs for icingaweb2, can you guide me specifically? By the way I use Ubuntu 20.04 operating system. Thanks for reading my question
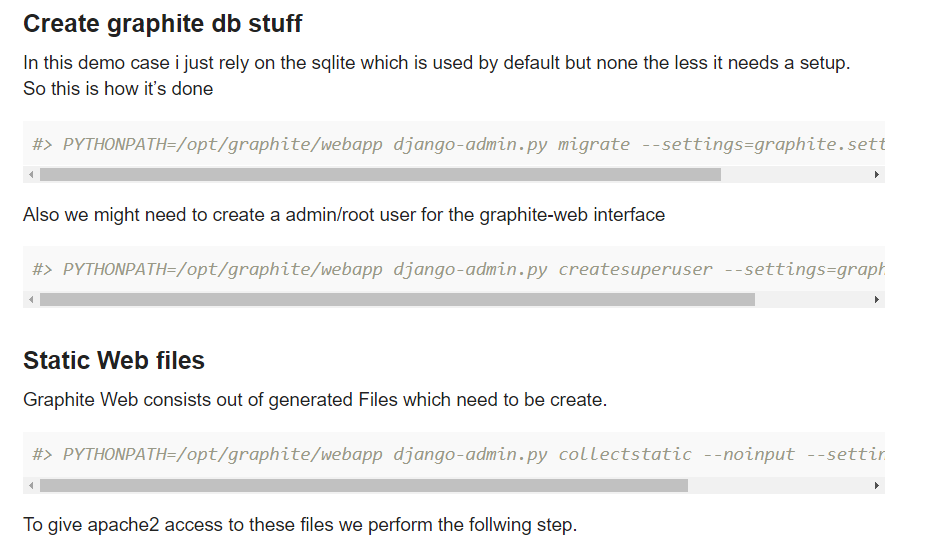
Have you seen this guide: Ubuntu 18.04 Bionic Graphite Guide ? It should be very similar for 20.04.
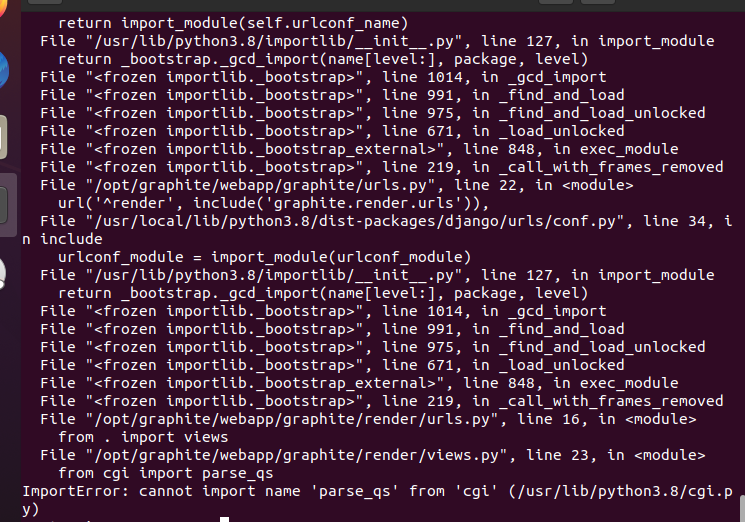
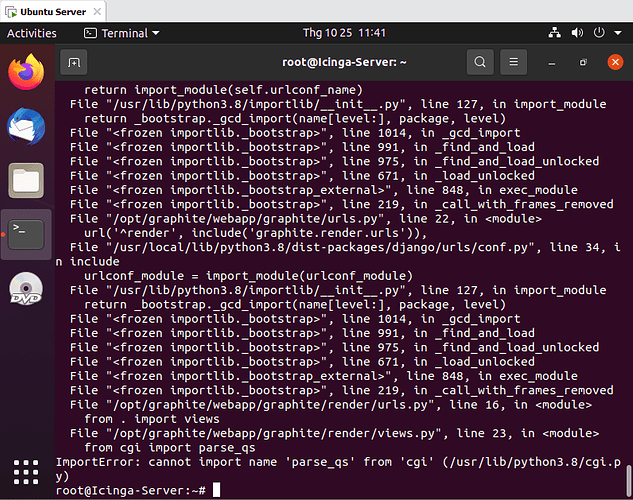
i tried to create graphite db tool then the command importerror
almost all PYTHONPATH commands are importerror
i am having problem at this step i don’t understand how to use the PYTHONPATH commands properly can anyone tell me.
Thanks for reading and helping me
Not familiar with the graphite stuff, but is there a requirements.txt file anywhere in the directory?
For Ubuntu 20.04 you will need to change the package names to python3-something because it is the default python version. At least that is what I remember from using this guide to install graphite on a 20.04 vm. Other than that it works.
@nvtu35
Iirc you should be good to go with this and then follow the rest of the steps
apt-get install python3-dev libcairo2-dev libffi-dev build-essential python3-pip python-sqlite libapache2-mod-wsgi -y
apt-get install golang -y
maybe you also need python3-sqlite , not sure there.